
Holy crap, CAT-man. Massive timeline kerfufflage today [and every day! See below].
Not seen it like this, before. Total timeline mayhem.
We were seeing and living in various timelines — and hearing them, which was trippier (always is). Hearing weird rumbles and huge swaths of sirens… then nothing… a few times over the past few days. Seeing weird people walking down the street then vanishing. Even a TWB ship saunter past then POOF… gone.

Saved by the Timeline(s)
Check this out. Some of us were totally saved by Guides today, manipulating timelines to keep us safe.
Some of us got together for a pre-Thanksgiving meeting, and relaized we were all needed to visit a local market for comestibles we were almost out of. On the way there, for whatever reason we dipped down to one timeline where we saw something — a car with a “dark” ca8al minion sitting there (his energy made him look dark), getting his courage up to do something — in the exact spot we stopped something bad happening a few days ago. We ran our errand, talking about this the whole time, and said on the way back if we saw that guy still there we’d swing around and confront him (in a quasi-friendly way)… ah, but the traffic on the way back as extra heavy for no apparent reason… and when we got to that spot, the guy (and his white Prius, remember those?) was gone.
Suspecting what was happening, one of the M’s immediately asked Guides if they’d slowed traffic to affect a timeline jump for us, to keep us out of harm’s way and they said, “Yup. Saving you from your higher, heroic impulses!” If this hadn’t happened, some of us probably would’ve been killed (either blown up or shot). Later, while doing some pre-Thanksgiving socializing, we again heard massive sirens going toward that area — just as we had last night — but then it suddenly cut out.
We keep living across, straddling, or skipping through at least four timelines simultaneously, seeing and hearing and experiencing all kinds of weirdness and crazy energy. We’re sure many of you are too, bringing with it all manner of (annoying!) emotional responses that have some CATs crying uncle.
Lisa Gawlas’ ‘Black Doorway‘
Some of you may have seen this today from Lisa Gawlas. Here’s an excerpt:
=============================================================
What came thru every reading over the last two days is this interesting, unique to each person, energy that is changing each person from the inside our and the outside in, each in its own way, targeting different areas in different ways thru each person, that started 11/11 and will conclude at the end of 12/4. This energy is having a profound, if not very unpleasant effect on many people, myself included. it is really ramping up our nervous system on so many levels.
Thru every reading there was this this (about 1 foot thick) black (my word) doorway to the right about 10 feet above the ground. We are all rapidly increasing in frequency thru this period. DNA is changing, brainwaves are changing, our nervous systems are changing, all in prep for our next great evolution.
The one thing I am sure of, that thick black door (which is not a door nor a gateway, spirit was pretty adamant about that, we have no name for what it is) will solidify the energetic changes that have taken place thru this energy influx. (They did put a dateline above the door of the 5th. I am grateful that is a Wednesday, a natural day off so I do not have to worry about not seeing!!) And yet, I cannot see what is on the other side, but so many people had heads up about 2019. How can the field be unknowable in December yet knowable in 2019. I will never fully understand this gig we call multidimensional life!!
The one thing I am absolutely sure of, 2019 is the year of change.
Can I just say, I am seriously over change!!
=============================================================
We’re right there with you, lady.
Oh, and in case you missed the latest GaiaPortal…


UPDATE1
MORE timeline jumps. Jeez. It’s neverending.




UPDATE2
FYI, we’re not in Kansas, anymore. Not even close. Factually, we have no idea where we are. There are SO MANY timelines skipping everywhere that you really need to stay positiv to surf over the tops of them as they roll past.
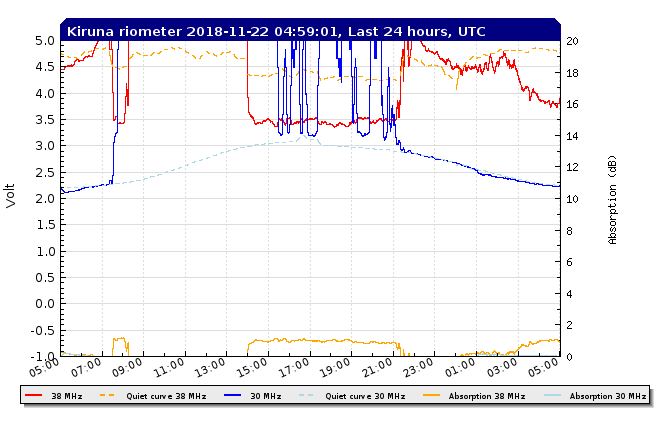
Kiruna has gone byebye:


Also, much of this video is the timeline jumpyhouse illustrated. Take a look:
UPDATE3
White squall time. A lot of us are feeling this latest one in the gut:




And timelines are REALLY popping. One of us watched as their S.O. got up from one room to go into the kitchen… turned away a moment… then saw them still sitting in that room — in an obvious timeline glitch. This is also why so many are having deja vu moments all over the place.

If last night was any indication, we’re all gonna need to BREATHE through all the incoming whompage.
More as we find it.



Uncle. Uncle! Uncle!!! Fo sho! 😭
I am 💯 going to have to navigate suuuuper mindfully with whatever is happening rn. Holy cow, Wednesday was excruciating – which is on the complete opposite side of my recent feelz. Yikes! My poor friends 🤪
I hope everyone else is fairing better than me atm 🤗
Happy Thanksgiving and be safe 💜
LikeLiked by 3 people
stay safe *cat’s*
I love you
that’s all I have to say
and yes yesterday afternoon UTC I was feeling very strange and my husband to
he was talking about temples he will build in the world for meditation….
I guess it’s on the new earth he he
it’s tricky cause he is spiritual but do not believe in soon ascension
I give not a rip on it and follow straight my ascension protocoll against all odds of my whole familly. When I will leave the ascension idea it comes up again like a cork in the water
so… * I know my way home…. *no doubt
my dragon painting is soon ready…. painting in the while Kiruna was getting crazy
much love to all here A.
LikeLiked by 4 people
i’m little, think i can squeeze in there with you? i won’t make a peep if you let me! ❤
LikeLiked by 2 people
Oh my goodness! I was going to post last night about this but totally forgot. Just after getting my daughter settled in bed I went into the kitchen and out if the window saw ( for a couple is seconds) a large black rectangle/door shape in the sky! Whoa, things are getting weirder!
Constant flashes of light, seeing dark shapes, sometimes the size of a spider, sometimes bigger. Blue and purple when I close my eyes, or a etc…
Sending more love and strength to everyone!
Phew thank source you Cats and Ms had that jump and are safe!
🙏🙏🙏🌟🌟🌟
LikeLiked by 2 people
Orbs etc… Must slow down my typing! ❤️
LikeLike
What an adorable sweetheart!
The first to celebrate 11:11 on 11:22:11.
FREEDOM accomplished.
LikeLiked by 1 person
The “Black Doorway” might very well be the Dark Cubus Construct.
Remember those many people in Mekka, circling around a black cubus?
Or some in israel, wearing it on forehead, when they pray?
It seems that some immature pupils, while in the school of the Creator-Source
of this Universe, initiated a game.
It was a game of hiding.
Like, hiding so well, Creator will never find them!
This is how the Dark Construct started.
Now –
In the Source Divine Mind there is only Love and Purity and Beauty.
Any concept of bad, or even evil, DOES NOT EXIST.
So, this dark game disrupted in a fraction of a second the whole Universe,
throwing it on a loop OFF the Cosmic evolutionary cycles.
It is my understanding, we are OFF 26,000 years. Universal years, that is.
In earth years seems to be much, much longer!
The dark game is now over.
It took eons upon eons of efforts, starting with the very Plan of Source Himself,
plus millions upon millions of Hosts of God from above and below, in final Oneness – to achieve Universal Freedom from this game.
On its own realm, this construct was switched off, annihilated, rendered null&void, totally and forever DISSOLVED.
What we all go through now, is the Manifestation in the physicality
of the process of Freedom, the Re-storation of God’s Cosmic Order.
The mightiest tool of our Victory was, of course, the Fire of Love from the
Heart of God. This mighty Love-Fire PURIFIES any possible dark energy
into Crystalline Light.
It is what Gaia Portal mentions, by the huge explosion in the Central Sun
of our Galaxy! It happens NOW!
When Lisa cannot identify the form, it is because the concept of a dark cube
construct does not exist. It was a sick invention.
When she sees it to “solidify”, it means it will be CRYSTALLIZED to Light –
which I see as – Dissolved!
That might well be the final Momentum of our Liberation – what many call Event.
LikeLiked by 1 person
I thank Source and all of our Light Being friends for keeping us all safe and on the right track.
I thank you, Cats and M’s, for this wonderful blog and everything you do for the betterment of us all.
I thank you, fellow commentors, for your insights and thoughts.
There is so much to be grateful for!
Hang in there, everyone.
Have a Happy Thanksgiving.
Love and Hugs to you all! ❤
~Sharon
LikeLiked by 8 people
https://wordpress.com/post/dandyliongreen.wordpress.com/191
at least it’s a soft squeeze ~~~
better than being stuck between a rock & a hard place
LikeLike
Those Schumann spikes, oh dear, I feel them in the chest, especially at night …
Just looking at that kitty in the armchair makes me feel better ❤
LikeLiked by 2 people
The flashes of light and odd sounds from out of nowhere I experienced yesterday are now making a lot more sense!
Thanks for the update Cats & M’s, so glad you are all safe!
Happy Thanksgiving 🍁
LikeLiked by 1 person
I was going to mention we must have jumped some serious timelines.
Last night I dreamt of my family and I leaving one large sea vessel to board another one. They looked identical.
Then we were in some kind of race. We were both still in harbour and trying to reach the opening to enter the sea. Fortunately our ship beat the other, but only just.
When I awoke I watched lightcodes fill my inner sight.
So glad you are all okay, your team is awesome.
Mark
LikeLiked by 4 people
So, I start my morning by looking out the window into what looks pretty appealing. The birds having breakfast at the feeder, the foliage shiny from last nights rain and a few patches of blue sky amongst the clouds. Then I bawled as I have done the last three days. Tears of release,sadness, and healing. Wow! Lisa reading next Monday. We’ll see. (or more correctly, she’ll see)
LikeLiked by 4 people
And now for something totally groovy, and today’s earworm (seems like a nice timeline!):
Hey, am I developing clairscent if my house is filled with the the smell of turkey but I’m a vegetarian?! Been smelling coffee, too, but don’t own a coffee maker. Weird, but kinda nice. Happy Thanksgiving, all!
LikeLiked by 7 people
Kolibri, I love this! Thank you so much for sharing! Made my day/evening 🙂 Light, Love, shine on baby! xxx
LikeLiked by 1 person
Oh, massive whammy song!
-CAT4
LikeLiked by 2 people
Wow, that’s just crazy. I had to re-read that part about what could have happened.
Was that someone specifically looking for you guys or wanting to cause harm to whoever was around?
Luckily you’re protected, thank goodness. So glad that you’re safe.
Please take care of yourselves.
Sending you much love.
LikeLiked by 4 people
I second that! Stay safe/protected (like I need to tell you that!) Noodles of love xxx
LikeLiked by 1 person
Hey, CATs! Even though my country doesn’t celebrate it, have a happy Thanksgiving, I’m sending you tons of love and light!
Things have gotten better here for us health wise, but I’m still going bonkers. So much energy flu, so many symptoms! I can take a timeline jump or a few, but this many is going to mess me up real good for a while.
I hope you’re faring better than I am!
LikeLiked by 1 person
Mm, we’re kinda all over the place. But thanks for the kind words!
-CAT4
LikeLiked by 3 people
Something happened this afternoon (Mountain time) and maybe still happening? On my way to pick up kiddo and as I was backing out of my drive way, started to feel “out of my body”! I felt I had no control of my suv and felt like I shifted…literally from one second to another. I stopped the vehicle to get my bearings, not feeling foggy, but sensing an energetic shift. I tapped into my inner self and said “your ok” and proceeded to drive. Tonight, I looked out to our night sky (boy, what is a gorgeous blue!), and I swear everything feels clear and clean…fresh!
Grateful you all are safe from the dark man encounter…I feel we are close to ending phase III and initiating the final phase. ☀️💕🌹🎉
LikeLiked by 1 person
*you’re ok…not your (dang you auto spell hack!) 🤦🏻♀️
LikeLiked by 1 person
feeling some could find bio-field tuning helpful in this now.
https://biofieldtuning.com/subscribe/ <— sign up and get a free session.
not my website. i dont know eileen and im not meaning to advertise… just feeling it could be helpful.
LikeLiked by 2 people
Yes! I gave myself a Reiki treatment (self care) last night, seems there was a shift; which I “heard” from my HS that our planet and an energy influx (galactic?) aligned.
LikeLike
BT basically defrags your energy field (releases old stuck energy) – lightens your load and helps you deal with life better, in my experience. Eileen is the real deal.
LikeLike
I think you’ll find that this is unnecessary now that we’ve gone to lightbodies. Given the energies we’re in now, all you have to do is WANT to change… and you will. POOF.
~M6
LikeLiked by 2 people
Just want, don’t have to believe / know / get it? I can see the folks on this site doing that, but is that the case for the general population? (Sorry, new here…)
LikeLike
I’ve had countless events of deja vu over the past few days.
LikeLiked by 3 people
Didn’t you just say that??
-CAT4
LikeLiked by 8 people
Sorry, we’re late in approving and replying to comments. We’re kinda wiped out (at least I am). Hopefully tomorrow will bring a respite of positive solidity to our existence.
-CAT4
LikeLiked by 7 people
Funny you mention this new timeline stuff, because this is what appeared last night. Mentioned your post in here for reference, too, because this ties in.
https://heliosjournal.com/2018/11/23/vision-of-a-fantastic-new-earth/
LikeLiked by 1 person
I dunno. They cite “Corey Goode” right up front, along with… Schrodinger’s OTHER Cat! (That must be the cat that didn’t make it.)
Few people realize that we represent the CAT that refused to get in the stupid box in the first place. 😉
-CAT5
LikeLiked by 4 people
Actually I had written down this dream. That last blast from a few days ago was really powerful! Definitely a timeline shift, and I was able to see what happened to that location described in the dream as that shift occurred within just a few seconds. That was the story.
LikeLike
We’re feeling them constantly. I for one didn’t think timelines could behave like this, in rolling waves. Must be a lot of awakenings going on, free will changing outcomes.
~M6
LikeLiked by 4 people
Hm. That is really interesting.
-CAT2
LikeLiked by 1 person
@ helios, please see this update from Rick Jewers and also see the video he posted few hours after that…
UPDATE
In 8 hours, an important Shift will begin. This Shift takes 12 hours to complete on Your linear Time. During this Shift, there will be many energetic calibrations individually. Collective Consciousness will expand further also triggering more Awakenings in the Others.
During this period, Realities will fluctuate and a state of neutrality will weed out and isolate confusion. A sequence of Events will coincide with this important Shift/Integration. You are reminded to remain in the highest discipline, not interfering and just allowing.
Some of You will be taken on Higher Consciousness trips into the near futures of these linear Timelines, to place certain Higher Energetic Design, that subsequentially, the linear timelines will attach to.in short term.
There will be Galactic repositioning during this period, in preparation for the next phase and events.
Love and Light
Rick .
LikeLiked by 2 people
“…not interfering and just allowing.”
This is probably why Guides sidestepped us and kept us from interfering on that one lower timeline we were straddling. Still, don’t be afraid to get involved when you’re out and about in the world, if you feel called on to do something positive. If what you do will cause problems, things will happen to stop you, otherwise… act accordingly.
~M6
LikeLiked by 4 people
Thanks for this, Mr. M. I miss seeing Rick’s messages since I was kicked off FB by the nasty folks. Tempting to open a new account and lay low.
LikeLike
It’s good to know that the *cat’s* are okay!!!
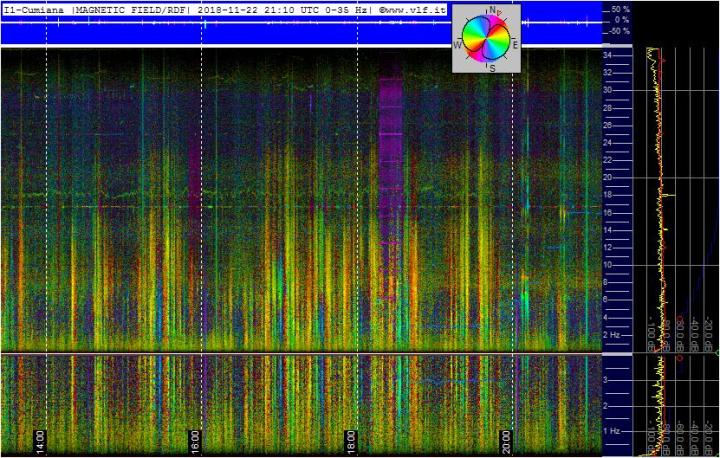
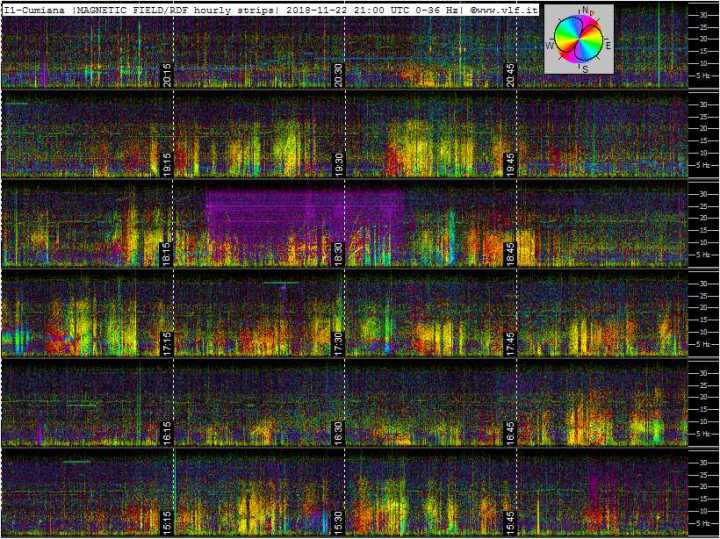
yesterday late afternoon again an energy attack… it was the Schuman and Kiruna
I felt a kind of cold in my upper body and went to bed at seven UTC
the Kiruna shows some strange images…
so I saw this today: You are not dying, it’s the Schuman Resonance
http://howtoexitthematrix.com/2018/11/09/youre-not-dying-its-the-schumann-resonance/
love A.
LikeLiked by 1 person
Note that the SR you’re seeing in that one chart (that we all typically look at) is the MOSCOW Schumann Resonance meterin Tomsk. There are local variations…
https://www.heartmath.org/gci/gcms/live-data/gcms-magnetometer/
…though Tomsk does seem to capture what most of us are feeling, most often. We so wish we could install SR detectors all over, but they’re a bit of a chore to contruct and maintain (it takes a university or college, and an SR enthusiast to run it). They are also big hack targets these days…
Oh, wow. A timeline merged over me as I wrote this! There were double words and word-and-a-halfs in the sentence I was typing!
~M6
LikeLiked by 3 people
why is GCI002 Hofuf, Saudi Arabia so different ? peaks are over 300hz?
LikeLike
That’s a combination of all the healing energy being sent to that region, along with the energy signatures of all those ‘feet-on-the-ground’ beings helping.
-CAT5
LikeLiked by 3 people
Happy fibonacci day, yawll!
Whadda night 🙂 The full moon appeared like a spotlight last night!
My Pleiadian friend has been locked into my field VERY strongly over the last couple days.
As she laughs.
love/light
LikeLiked by 1 person
See! I posted in the last post that this exact thing would happen. Major timeline stuff nov 22nd. Nothing dark only amazing light… we have to stop whining about the dark and focus on love!!! Meditate don’t hate!
LikeLiked by 2 people
I spent A LOT of time programming computers this time around. Pretty much several hours a day since I was 8. I could sense that there was something in there that I needed to figure out. And I did, I developed an excellent nose for artificial “intelligence”; which is what the ego boils down to.
These days I instantly recognize the energetic signature that people emit when they slip into computer mode, and all the ways our society is designed to program us just like computers. TV programs, Radio programs; wherever you see a protocol, step by step sequences (we call that procedural in programming lingo), loops.
Having spent all that time learning how it fits together, it started feeling like an obligation to leave the field in better shape than I found it. And leaving I am; I did my part; once we’re out of here, I don’t want to see another digital gadget for at least a thousand years.
So I spent the last two years designing a new programming language with a focus on making programming more humane. I’m pretty sure that programming computers isn’t for everyone, it’s seriously hard and frustrating work. This is not about teaching everyone to write code, it’s about adding a touch of Source to the lifes of those who choose that path for whatever reason.
https://gitlab.com/sifoo/snigl
There, done; now push the freaking eject button already!
~Sifoo
LikeLiked by 3 people
My cat woke me in the wee hours for a feeding (which she does every night since my husband got her on that schedule). I was EXTREMELY disoriented without clue as to the day, time, or if I had already fed her. Instead of contemplating whether I had had a stroke or not I just fed her and went back to bed. Kept reawakening to fine vibrations throughout my torso. Finally woke up in the morning feeling clear and great Assumed large timeline jumpage. Cay
LikeLiked by 4 people
Has anyone else seen the strange green colour around the moon?
LikeLiked by 2 people
When it first rises, or high in the sky? What region are you viewing from?
-CAT Eds.
LikeLike
I am in the UK it was about 8pm
LikeLiked by 1 person
Yes midweek in the UK there were halos of green, yellow and purple around the moon. I watched for quite a while. Tuesday the moon was huge as it started to rise.
LikeLiked by 2 people
Some of the biospheres are as large as Earth.
The consciousness streams (denisities/dimensions) are merging on schedule.
LikeLiked by 3 people
Ugh! Totally feeling “off” tonight. And the ear ringing… can barely hear the 3D world. Is shit happening?
LikeLike
OH yeah. Big time. Check the latest update.
-CAT5
LikeLiked by 1 person
I feel like this cat looks…
LikeLiked by 5 people
Great, now I’m almost falling out of my chair from laughing; it’ s like Edvard Munch designed his own cat.
~Sifoo
LikeLike
Unbelievable!
This is not funny. This cat should not be made fun of, would you laugh at children who are born with deformities from depleted uranium. I hope not!! The guy is a complete and total A-hole and you, Consciously Connecting and a few others here, are just as bad and anyone else who thinks this is funny. So, much for being enlightened!
Do you think you’d laugh at star family members who don’t meet your criteria of how beautiful someone should look? This beautiful cat is still one of Source’s creations, when you make fun of it you make fun of Source. Ask yourself why this cat has deformities? Maybe it’s parents were brother and sister, or the mother ate something that was tainted, or who knows, just look at the shit in our sky, all I know is that it’s sad because this cat may not have a home or someone to love it, like this heartless POS.
I expected different responses here then what I saw. You should be pissed off at this stupid man for being such a f@%king idiot, if anyone is ugly he is for not considering this animal is from Source and there are probably reasons for it, maybe to prove how INCONSIDERATE and MEAN people are to Beings that are different. There’s a lesson here, learn it!
Cat’s I hope you print this.
Disappointed
LikeLike
Why are you angry? I do like the kitty, if I could I would take him/her home.
What’s wrong with liking this kitty?
It’s the man who’s shouting at him that is ridiculous. He is the laughing stock, man!
This is some misunderstanding …
Love,
LikeLike
Consider the fact that you will be held to the same standards you judge others by, any millisecond now. Any moron can find faults with others.
I’m pretty sure that what most, like me, found hilarious was that the
cat looked so terrified for no good reason.
I don’t think you’ll find many who are not familiar with being different and being treated differently in here. If we couldn’t laugh about it we would already be gone.
~Sifoo
LikeLike
I wonder if I am straddling different timelines … When I write, words appear that I haven’t intended to write down … as if someone else is typing …
I look at the screen, wondering what’s going on, delete everything, and start anew … Once I even accepted the “other version”, it seemed better.
… Phew!
(I wish I had an appropriate image of a disgusted kitty…
https://www.google.bg/url?sa=i&rct=j&q=&esrc=s&source=imgres&cd=&cad=rja&uact=8&ved=2ahUKEwjm1bvI-OzeAhWJ_qQKHddmBn4QjRx6BAgBEAU&url=http%3A%2F%2Fwww.suzionline.com%2Fkedi%2Fkedilerde-kisirlastirma%2Fattachment%2Fdusunen_kediler%2F&psig=AOvVaw3ZYOmL8D2_–qyAypjQZQc&ust=1543145526121004)
And yes, the only thing that helps is breathing through this whompage 🙂
LikeLiked by 1 person
Yes, this is happening to all of us.
-CAT Eds.
LikeLiked by 2 people
Our kitten was in two places at the same (well as close as we’re going to get) time today. Pretty neat trick if you ask me 🙂 She snuck by me down in the hallway on the bottom floor when I opened the door, and when I turned around she wasn’t there. So I called her name and a furry head popped out of her basket upstairs.
Either that or we now have two kittens; and the latest one is exceptionally good at hiding.
I’m done trying to keep this ship straight, straight just went Dodo. This is some kind of quantum whitewater rafting, straight is the worst possible focus at this point. Whatever will be.
~Sifoo
LikeLiked by 3 people
I saw TWO of my mother-in-law in diff places. Even one is too much. 😉
-CAT5
LikeLiked by 1 person
Hahahheheha.
LikeLike
Hope he does’nt kiss his cat with that mouth! I Am in peace today, Happy Saturday!
LikeLiked by 1 person
Bubba, you guys/gals must be feeling AWE–SOME , looking at schumann
http://sosrff.tsu.ru/?page_id=7
LikeLiked by 1 person
Maybe full of AWE i.e Awe-full
LikeLiked by 1 person
Today, here in the country, it is deafeningly, stupifyingly quiet! Talk about peaceful. The only sound is the river in the background and the occasional cheep if the birds. I vote yes for this timeline!
LikeLiked by 1 person
Man, I totally dig that cat in the opener image. What would be great would be if the cat in the wall photo had a photo of the same cat over it’s shoulder, too.
LikeLike
I’d always want to be update on new posts on this website , saved to favorites! .
LikeLike