
We would like to take an Equinoctial moment and make a direct WRITTEN communication to the Spirit/HO ET side (HO= Higher Order), just to be very clear, and share it with the rest of the class. We didn’t want to make this an official post, but it seems necessary.
Most of us here have read Sophia Love’s latest newsletter (which we can’t seem to find a link to). In it, “One” asks us to become… One, and to become the new leaders of the human race. This is a fine sentiment, but our numbers are too small. There are billions of brainwashed people (representing requisite zombie portion of the collective) who can’t get out of their own way — and worse, there are people who know that they’re to wake up, but do not.
Sophia’s One asks us to “become the crazy ones.” [sigh] Well… we’ve kinda already done that. EVERYONE thinks we’re crazy! The normies and lots of folks in the “Atlantis” crowd. We’ve pushed the boundaries… and we keep getting censored, and our information removed and restricted. Then there’s the Beloved crowd shoving hogs for moolah. Folks, there is a sizeable portion of the population that wants to remain asleep, free will and all that, and a growing mass that likes them asleep.
It feels like we, as a group (all humans)… are stuck, or in a holding pattern. Indeed, some bloggers are now saying that there will be no SHIFT of the Old and the New Earths; some are saying that there is no New Earth and other things that aren’t true, and are falling prey to various beings who are impersonating the light… ones who are getting better and better at providing divisive messages and actions. Everyone wants to know if something is true or not, when they KNOW it’s all illusion and tat the only truth is literally THEMSELVES and SOURCE. Bottom line, we’re losing momentum as a group-entity.
The CATs feel like we (the Human Group we) get teased constantly by Spirit, get little blips of ascension energy… like we’re some kind of spiritual lab rat (which we are)… but then we get stuck. Raising the vibration of a whole planet was a great idea, but the project needs a Big Push to get over the dark hump that’s in the way. It feels like all this was supposed to happen faster, but some factions are doing a good job at intentionally slowing things down, and perhaps Spirit has also slowed things as well in a kind of wait-and-see mode.
Don’t wait and see, anymore. Speed things up.
Those of us “ascension enthusiasts” are doing our part, we have been for a while now, but it’s not enough. We are too few. The Spirit/HO ET side needs to do something more obvious to this level, otherwise we’re gonna sink back into the old pattern; even then, the darkness has PR teams ready to convince people that whatever happened was something else and that they need to get stoned and go shopping. Perhaps if Spirit/HO ETs got rid of/relocated the dark factions, in the interest of the whole, things would progress more naturally. We still see dark magic being used to hold people in its web. And while more people are indeed awake, they simply do not know how to “take back their civilization” without being marginalized into ineffectiveness — or worse, into extremes of behavior… extremes which we’re supposed to be migrating away from. We are spiritual adepts, not shock troops. We have little capacity anymore at being angry villagers. Mobs settle nothing.
The issue too is that we can only bring awareness to the situation, but it takes a lot of internal work of the individual to help create change, as well. People can be dragged into the Change-River, they have to want to drink… and some just aren’t ready.
It’s time NOW for humanity to split into two learning platforms. We’re pretty sure everyone knows what those are. Something BIG needs to happen to get us over the hump. So… let ‘er rip.
Our two cents.
Please keep meditating. It seems to be all that’s holding our heads above the fray.

UPDATE1
Well, perhaps real change is on the way… perhaps. Here’s a new flare and CME. Effects? We’ll see:




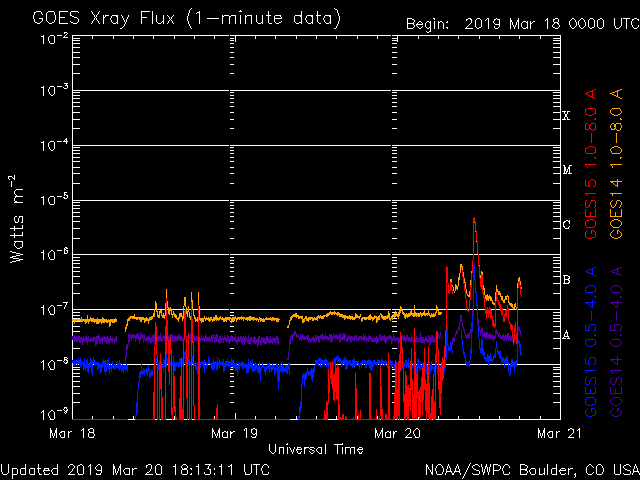
UPDATE2
What’s most interesting about the recent CME is the missing frames from the satellite recordings:


Now look at this:


UPDATE3
We mentioned this in the previous post, but here it is again. We noticed a muonic correlation for the previous timeline jump. Check it out:
UPDATE4
Ah, there were actually two flares/CMEs. The satellites aren’t showing them all:


UPDATE5
Looks like that first flare/CME is just starting to hit. No idea as to the effects.


And there was more activity lat night:



Wow, look at the blast on this solar time-lapse. Blam.
And this timelapse of that jupiter-sized ship monitoring the flow coming out of the sun. You can see its sensor beam projected into the sun’s flow.
UPDATE6
Getting worse. Some of us have headaches.

UPDATE6
And our fav muon detector is back up, finally, showcasing what we already knew about the timeline jump on the 19th:





And NO, Spirit and Guides, this does not mean that we want you to axe a few CATs to make us grow any more. We’re grown, thanks. We CHOOSE to grow elsewhere. Other people’s free will is starting to chafe. We don’t care what the old agreements were. Hang the old agreements! We ask for the new learning platform, free of the “old evil.” If a whole universe can be created for Madonna as a waitress, then we can certainly have one where those like-minded people can go to a bright green New Earth — separate from the Old Earth, which we were promised in our between-life carrot package — and learn in a new and exciting and SAFE and non-polluted way.
-CAT Eds.
LikeLiked by 17 people
Ditto, ditto and DITTO!
Would it help to all meditate at the same time, give it all we’ve got?
https://fm144.blogspot.com/2019/03/march-equinox-meditation.html
Time for the SHIFT, no more procrastination please. Love, Light, Peace 🙏✨❤️
LikeLike
P.S That CME is amazing, hope it actually is a game changer, for the positive! ❤️
LikeLiked by 2 people
Lily, you couldn’t have chosen better words!!! A game changer is exactly what happened last nite around 9pm! The “me” of the ONE is really a group of “Ones” that becomes a WE! The new physics is 1+1=1 🤗 Hang in there!! Divine Intervention is REAL! Blessings to all from the Cosmic Correspondent!😇
LikeLiked by 2 people
@ Nancy, yes hanging on! By looking at these updates, that ship, that blast, things are looking up again! Much Love ❤️
LikeLiked by 1 person
P.S Please ignore the words ‘Galactic Confederation’ and ‘Light Forces’, I just thought the meditation might be helpful in some way….Peace ❤️
LikeLike
@ lily144
Sorry to say, lily, but the “144,000 Starseed meditation” is hijacked.
Better take the reigns yourself, and just intent to unite with us, in Truth.
There is A LOT at stake, this last battle seems fierce to me.
LOVE to you, lily.
LikeLiked by 2 people
@oro thanks for letting me know. I was guided to just light a candle and meditate as I usually do, thought of you all whilst I did this ❤️ Apologies to everyone for posting a link that was not so good! Love to you Oro and all 🙏
LikeLiked by 2 people
Thank You Cats & M’s … Yup we be the crazy ONES, I 2nd that 🙂 something needs to shift big time “sharp left” the split … over the half way mark, we have made a choice & straddling both worlds is a challenge everyday something has to give we have worked damn hard to get to this point … let er rip – give it to me baby ahahaha 🙂
something has to give we have worked damn hard to get to this point … let er rip – give it to me baby ahahaha 🙂
Fascinating on my way to work this morning I saw a car number plate CME 01L … could it be that it will be like OIL … the oil slick we need? either way I feel a shift coming an inner excitement bubbling … holding space for all filling with sacred love.
the Sekret Tree Project? very interesting spirit showed me a new healing way with trees, communicating with a tree & the tree assisting in the healing knowing what is needed whether It is in the roots, the trunk or the foliage & so much more. Trees are like Oxygen to a starved soul 🙂
I am the One, I am Love!
LikeLiked by 3 people
Thinking this also seems to get rid of them: https://m.youtube.com/watch?v=pxvzEfI0BFU
LikeLike
Not sure if Spirit anticipated this post, but there was a CME a little while ago:
Won’t officially hit till… say the 24th… but we’ll probably feel its effects soon.
-CAT Eds.
LikeLiked by 11 people
Whatever this bout of programming is, it will hit the earth dead-center.
-CAT12
LikeLiked by 11 people
Well said Cats!
LikeLiked by 6 people
in same boat…
https://en.wikipedia.org/wiki/Non-cooperation_movement
LikeLiked by 1 person
Deep Bows for speaking up and no doubt BEing heard aka CME! Pondering the same the other night of course, BEcause WE ARE ONE Now. Then woke up with a song saying ‘it’s all a dream’. More are reporting seeing brilliant Green in our 3rd eye consistenly Now.
LikeLiked by 4 people
No, the flare/CME happened BEFORE, we just didn’t notice it. Spirit may have anticipated us, or we’re just being slow. We’ll see wat happens in the next few days.
-CAT Eds.
LikeLiked by 4 people
Thank you!
And that CME… woah! 🙂
LikeLiked by 1 person
Hear, hear!
Let’s do this.
See you all on the other side.
LikeLiked by 5 people
Like it or not CATS, you guys r leading this train, the go-to guys for all things EVENT or shift, NE, even NEBRASKA, so with that, sometimes you gotta coach the players back onto the field to get them across the goal line with a winning and motivational speech! Rally the troops to meditate! A lot of us look to you for CATS for signs, encouragement and hope. We can’t read those meters. Lol. And some of us came to the game late so our meditation skills are lacking compared to others. Stepping up meditations now!
LikeLiked by 13 people
My sentiments ABSOLUTELY.
LikeLiked by 3 people
Honestly, if they just helped us get rid of Team Asshats, I would be perfectly fine with anything else that came after. I’m just sick and tired of their shenanigans. I want to live in peace with all my friends and loved ones. Is that too much to ask for?
Speaking of which, shoutouts to that incredibly brave kid who called the police on that insane Senegalese man who attempted hijacking a bus with over 50 school-aged children in it this morning, in Milan, and then set it on fire. They prevented a much greater disaster from occurring.
I feel that they were saved by some timely divine intervention.
LikeLiked by 9 people
Yeah, I also knew the biggest hurdle for this planet Ascension (I hate this word too, reminds me of new age charlatans) wasn’t the darkness- it was the normies. 😱😱
LikeLiked by 2 people
Thank you. ❤
I was starting to get worried that I had missed the boat and had been left here, on the not-so-nice world whilst all of you had left and were in paradise. This post has assured me that there is still work to be done.
LikeLiked by 3 people
Growl, hiss!!! Youse said it all. The only thing I can state unequivocally is that I really did see the pink-lavender halo around the sun, so something is up!
LikeLiked by 7 people
I saw this during the equinox:
It was wonderful.
LikeLiked by 5 people
Wow! Amazing! I wish I could see it too!
LikeLike
You say, We are too few.
But you know that a very small percentage of humans of higher consciousness/vibrations is needed to change this paradigm (I forgot the exact percentage, it is very small indeed).
The most important thing is to learn all about us, to understand that we are very, very powerful beings, and only then we can move into higher vibrational levels.
In case you want to read Sophia’s message, here is the link:
https://www.sophialove.org/ge-blog–comments (scroll down to Update 1)
I personally do not resonate with the above message.
Life is breathtakingly beautiful …
White pelicans:
Love,
LikeLiked by 8 people
Which above message? Sophia’s or ours?
We understand our power, but we cannot lift an entire population without a certain spiritual mass… and we’re seeing inertia settle in.
-CAT Eds.
LikeLiked by 6 people
I wrote above:
“In case you want to read Sophia’s message, here is the link:”
I was also talking about the spiritual mass needed.
Love to you,
LikeLiked by 2 people
@ antoniatailor
We need to pay great attention.
The Sophia message you gave the link for, is COMPROMISED.
I can’t find the real, genuine message link, either, but this is the title:
“Sophia — Removing the chains of allowing.
March 14, 2019, 2:22 AM” (It is I. It is One).
Sorry to say, but the “144,000 Starseed Meditation” is also hijacked.
No wonder so much confusion! / inertia!
Yet, we can always unite in the one moment of NOW, in meditation, by simply stating our intent before we start. And count on our own, in DIRECT connection.
“The present is the only time there is”.
(A Course in Miracles)
LikeLiked by 4 people
“Today is a gift, that is why it’s called the Present” 🥰
LikeLiked by 4 people
@oro what you said about the 144,000 meditations had me thinking. Last year, I joined a mass meditation, I am pretty sure it was this one and got quite badly attached whilst trying to do it! At the time I thought it was entities trying to stop me from me from meditating, now I realise it could well have been a ‘dark’ meditation that was, like you say ‘hijacked’! Explains a lot! Thank you❤️ Feels like this blog is the only place (as well as your own soul/spirit/guides/higher self) that is safe and real! Peace 🙏
LikeLiked by 1 person
That “144,000” thing is crap. There is no magic number.
-CAT Eds.
LikeLiked by 7 people
Dear CATs and Ms,
I am sorry for posting Sophia’s link. This was an uncalled-for request, and it led to a misunderstanding. I did it because you wrote most of you had read “Sophia Love’s latest newsletter (which we can’t seem to find a link to)”. Sorry. This was the link I found, but you hadn’t asked for it. Years ago I decided not to offer uninvited advice.
Let me repeat: I do NOT resonate with Sophia Love’s message.
Thank you.
LikeLiked by 2 people
Oh, that’s ok. We’re glad you found it so others can see how it’s a little… off.
-CAT Eds.
LikeLiked by 3 people
Dear Oro,
There is a misunderstanding.
Please read my comment to the CATs and Ms.
Thank you.
LikeLiked by 1 person
@oro
Why do you say the message was compromised? The link in question is pointing to new messages from Sophia’s old friend “The Guardian (GE)”. I can’t find any hint or article that would confirm what you said or do you probably refer to other messages?. Can you please clarify this, or post a link, so I can check for myself, please?
Thank you
LikeLike
mmmrowl – yes inertia. The purrfect word for it. Most of the ONEs I know who have been on this journey for so many years are feeling the frustration of the seeming “empty promises” of (it’s really coming soon) ascension, and the chaos around us with the normies. We feel alone (because most of our families are normies and think we’re furry nutballs and they don’t want anything to do with us), finding commonality is difficult in the community because it’s not easy to walk up to someone at random and talk about all of this “fun”, and “they” keep disrupting our sleep and our health, so we’re just plain tired and discouraged. So … the only easy solution is to simply curl up in your catball and take a nap. Inertia indeed. I’ve always been an adventuresome little kitten, but lately I oddly feel like I’m morphing into an ostrich who’s looking for a bucket of sand … YOUR space is the only place I feel NORMAL these days. miew purr … now, if we just had some catnip tea.
LikeLiked by 5 people
Thanks Antonia, Minky & I Am with You. We Are Unlimited, w/Much Love to All. Peace.
LikeLiked by 3 people
You are most welcome ❤
LikeLiked by 2 people
@ antoniatailor
2019-03-21 AT 5:21 AM
hi, antonia,
sorry for any misunderstanding!
Didn’t mean to harm anybody in anyway.
Wanted actually give some info I found important, to all readers, in fact.
LikeLiked by 2 people
@ Mr K
yes, i found Sophia’s mail – message:
“Sophia — Removing the chains of allowing.
March 14, 2019, 2:22 AM” (It is I. It is One).
from One, true and wonderful.
Then, reading her Newsletter with the Guardian message, I noticed it states quite the opposite of all we all know to be true. It shocked me a bit, so I had to ASK. The answer was that message is not true. This is how I was so sure, thank you.
LikeLiked by 2 people
The pelicans make a sharp left turn. 😉
LikeLiked by 5 people
VEER LEFT! HOIST THE THING!
-CAT5
LikeLiked by 6 people
I have noticed a lot of folk taking pictures of iridescent images/clouds in a sunny sky. They believe it to be a sign from spirit or suchlike.
I’m convinced it’s the sun light catching the particulate from the Chemtrails but don’t have the heart to tell them.
Then I keep reading of many people saying they have visions of the EVENT. They are saying before the flash of light, the sky is filled with iridescent clouds.
What if, one of these CME’s is so powerful, it reacts with the Chemtrails to create a sky filled with iridescence.
What irony, that the pre-event energy/indicator is a sky of rainbow clouds, thanks to the twats who are trying to block it!
Mark
LikeLiked by 5 people
Whoooaaah!!! Here it is:At approximately 1:45 PM PDT, I was working in the garden when I HAD to go in. I could barely walk and only with the aid of my cane. I went to bed and from about 2:00- 2:50 PM PDT I thought I was dying. I became freezing cold, my body felt buffed as if I were in a rapidly moving stream, the whole top of my head was raging heat and 2/3rds of my physical body was empty. (Now I must say that it was a most interesting experience.) Anyhoo, I’m now back. The only remaining sensation is tremendous 3rd eye pressure. Time for my afternoon latte. (Just another day in Paradise)
LikeLiked by 8 people
as I write this, I am seated next to the window where some faceted crystals send rainbows shimmering around the room. I gaze upon one spot where lilac colored fabric hangs, and there are RAINBOW COLORED PRISMATIC CAT PAW PRINTS glowing on the fabric! YIPPEE YOO HOO!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
yesterday as I looked at some other informational video on u tube, in the lineup to view next was an Abraham hicks video about cats! Oh my, then after watching several of these, I watched a few more AH videos about just staying in joy and letting the universe do its part.
I felt like spirit is shouting out support for me/us.” just remember joy, remember what you want! you are an eternal creator”
usually, when we are SOOOO close to receiving something is the most intense of the experience. yes, we are all exhausted and worn out beyond belief.
may we continue to point our vision on what we want.
feel the joy and pleasure of New Earth, wherever we are, wherever it is located and wherever you may be upon NE. and all the moment to moment changes which happen there.
the more we focus on what we DO WANT,
let go seeing what we don’t want. which for most of us is the ca8al and company.
SO here are the cat videos. for a bit of cats as helping us to remember.
I know the CATS here prefer not to insert video, yet I cannot share the title without the page coming up too. for some reason.
think like a cat (2015).
other Abraham hicks excerpts about cats:
(the first two–‘understanding your cats behavior’ and ‘think like a cat’ are the same person talking/same excerpt).
the third one is so right on, too
https://www.youtube.com/results?search_query=abraham+hicks+cats&sp=mAEB
feeling goood no matter the circumstances:
LikeLiked by 5 people
in that above post, I inserted two links to the Abraham hicks cat videos, yet the one video about feeling good no matter the circumstances shows up twice. OKAY!!
here is a link to the Ah cat videos:
https://www.youtube.com/results?search_query=abraham+hicks+cats&sp=mAEB
some great humor and insight for us all.
blessings to all.
~~~~~~~~
for a number of ‘years’ I’ve been aspiring to focus on
WE ARE ALL MAGICAL
WE ARE ALL AMAZING
WE ARE ALL POWERFUL
WE ARE ALL LOVE
I even made this into a song to sing over and over.
others so inclined might use this for a chorus of the song, and create verses, too.
I’d love for anyone to share their verses if the do create them.
LikeLiked by 5 people
As We have been told, It is All Ways darkest before the Dawn. Peace.
LikeLiked by 4 people
@Christopher, thank you for the reminder, much love ❤️🙏
LikeLiked by 4 people
Have been meditating pretty much all evening on and off. Off to bed but just wanted to send my love to all ❤️
Moon is super bright! Also noticed a plane chemtrailing vertically in the dark night sky! What is that all about?! Curiouser and curiouser! Sweet dreams ✨❤️
LikeLiked by 3 people
A-effin-men CATs. I wholly endorse your message.
LikeLiked by 2 people
I know we are all on the path to move forward and also move into a new adventure where suppression and manipulation is no more. What I picked up in the last week has really opened my eyes and mind about the “event” and current state. First, I stopped reading Sophia’s blog because the information became redundant. I really like her and her past work, I think if you are new to this info, she is a ‘go to’ up to a point. Second, without any disrespect to anyone in this form or anywhere else, as I recognize we all are uniquely on a path of discovery and expression. But we have to go WithIn if we are going to see any change, like real change! There are a lot of people awake, but many who are-let’s say who are almost wake-do need a physical event to trigger a response. I feel that the physical response piece is very close. BUT, I’m picking up constant manipulation on all fronts, including channeled info (we knew that already) but what’s more prominent is people (those who await on verbatim of the channeled messages) should stop engaging channeled messages and listen to their own guidence! We will never own our experience or make real change until we acknowledge the power we have, independently and collectively. With all the shifting (timelines etc) that is increasing in occurrence and frequency (vibration), going within, grounding and establishing a relationship with your internal self will bring the real change. Tomorrow can’t happen today, that is the true gift, being present is the present! In the quantum realms, everything has potential, and exists at once because there is no tomorrow or future.
My focus on change for all on this gorgeous planet, is Balance! Bring balance between patriarchy & matriarchy, control & submission, consumerism & conservation. Look to love and respect, kindness and peace. Everyday my meditation is a moment where we have achieved that. AND I got my confirmation that day (previous post) running errands. That was my “oh mah gawd” it’s working moment! I look back on all my past experiences – the sliver of sight into the veil, the space between atoms that made up the color of a flower’s petals, to what zero point felt like. I realize more than ever the gratitude and appreciation is the ignition to the perpetual manifestation of the physical…thus, I give my deepest appreciation to all of the Cats, to all of you who post here and to those who are in observance…we all are making a difference! I know we are not giving up…just go within and start connecting with YOU. ❤️🌹❤️
LikeLiked by 8 people
@NLN8 thanks for your comment. Have pretty bad PMT at the moment and everything feels so bleak! I’ll find my light again and I’m starting to learn to look within rather than seeking solutions outside! Much love ❤️
LikeLiked by 6 people
You don’t need to find your light, you are a beautiful light! 💕☀️✨
LikeLiked by 4 people
@NLN8 thank you so are you 🙏 a beautiful light🌟 gonna start blubbing, gosh my emotions are all over the shop! ❤️❤️❤️
LikeLiked by 4 people
Oh yes @lily144, beautiful light inside…it is easy to sense that. You are made of beautiful and powerful light. 🌞☀️💫✨⚡️
LikeLike
Great post. NLNL8! It’s true and I’m going to tack on my own message here as well. We all need to find our sovereignty and that is the ultimate paradox. All this god worship and celebrity worship and sports worship and whatever other worship should be directed towards worshiping yourself and the people around you that make a difference.. And not in the egotistical kind of way. That’s a different thing… I’m talking about putting your faith in yourself and others like people do with the “guy in the sky” and other beings you’ve never personally seen or talked to. It ain’t about them otherwise we wouldn’t even be having this conversation.
It’s about people going inside and becoming conscious of all the unconscious behaviors they’ve been playing out without even really realizing it. And then the hard questions come, like… “Why am I doing this?” or “Do I really believe this thing I’ve been so rigid about?” or maybe “Why am I doing things that are not really me or in my nature?” – The questions get deeper the deeper you dig.
What you will come to find out if you ask enough questions and you’re truthful with yourself… You’ll find that most of your life has been about living someone else’s fantasies and not really your own. You’ll find that basically your whole life has become one big game of pretend and you’re tired of being a pretender.
Beliefs are just thoughts and thoughts are just that… thoughts. They can be anything, and usually negative from the conditioning, so what are you making your thoughts mean to you? Because they don’t really mean anything until you make them mean something. This is why you got to align yourself with positive thoughts and what you truly want because thoughts are like magnets.. they attract like minded thoughts. Garbage in = Garbage out.
Love all you guys and I appreciate every single one of you!
LikeLiked by 5 people
There are two kinds of worship that are worth the effort; truth and love. Anything else leads down the drain. Icon worship, funny how many old sayings actually carry profound truths once you gain enough experience and perspective.
I’ll just note that you have to want the right thing as well, otherwise you go back in the dishwasher until you do. That’s the funny thing about free will, you either align it with Source or try again until you run out of options.
Same, same!
~Sifoo
LikeLiked by 3 people
Don’t think for a second that I don’t want this to be over yesterday.
But judging from the stuff I’ve been processing lately we’re still warming up for the big whatever, and we’re going as fast as possible.
I have a feeling many are simply waiting for the collective, because they’re not capable of carrying truth by themselves yet. It’s easy to forget what kind of ninja skills it took just to get this far. Once they feel safe enough, they’ll make the right choice.
My antennas say that some kind of trigger is right around the corner, and a whole bunch of people are anxiously waiting for the test without being aware.
~Sifoo
LikeLiked by 9 people
@Sifoo, I do hope so, much love ❤️
LikeLiked by 1 person
Here’s the thing though… Bloggers and whoever can write what ever they want to write but it doesn’t change the fact that their post is ONE perspective amongst 7 billion + perspectives down here. Everyone has a little piece of the puzzle here and when people write things so matter of fact-ly like they have all the answers, you’d better be careful what that info is really about. It can throw you off the trail for years. Also, when you open yourself up to different beings to just “chat” and you don’t know who or what you’re connecting to… Yeah, good luck with that BS… Operators are always standing by… And not the ones you think they are. Perception/Deception filters my friends.
I’ve said it before… It’s about us down here, not all the other beings entangling themselves in this web. Think about this for a moment – There’s a whole universe out there, multiple ones in fact… A vast array of infinite possibilities… Yet, you got all these beings and species over here getting involved in this bullshit doing whatever they’re doing… Now you got to stop and ask yourself, “Self? Why would that be?” There’s a lot of good questions that people aren’t asking right now.
I know the new place we go is pretty dope because I’ve seen it. So I don’t know what mofo’s are on about. I’ve seen the visions and that’s one of the things I’m supposed to input in my music. So yeah… Nothing is gonna change that and I devote my life to getting us to this new place I’ve seen. So you can run and tell that, homeboy!! (Bedroom Intruder reference for humor impaired)
LikeLiked by 10 people
Completely grey sky for 2nd day in a row. Weather forecast said sunny all week.
More honking on the street, newspapers getting ever extremer in their version of reality. More zombies walking the pavement.
Neigbours are shouting as I write this.
Woke up at 1:30am. There was a black creature that attacked me, had the shadow of an armadillo.
When it tried to bite me, I clenched its beak, which looked like a crocodile, with my hands. Then a small dog came and took it away.
Armadillo came back and once again I clenched its beak and the dog came to take it away.
Armadillo came back for the 3rd time and I stabbed it in the head with a knife, head was really small like a bat. I completely cracked open its skull from top to bottom and split it in half yet it wouldn’t die. It looked like an ugly gremlin. They are extremely ugly already so this was a winner.
Then I woke up.
Fell back asleep at 3:30 and dreamt about ufo’s and aliens. Felt like an invasion, didn’t feel right. I was relax yet it all felt wrong.
Neighbours still shouting.
Yesterday had an ear thing twice: no sounds but I did feel something in my ear. Like a wave but soundless. Difficult to explain.
Just now had a wave with sound in my right ear, like turning the volume up and down for 3 seconds. Like those hearing tests. Different from the usual ringing.
Neighbours still shouting.
I’m wondering if it’s an African cleaning lady talking on her cell phone cause I hear furniture moving. Why do these people always shout when they talk on the phone? Do they not understand the concept of a telephone? Do they confuse it with a loudspeaker?
I’ll ask my nephews they are half-Ghanaian.
Yes, it’s the cleaning lady. She’s vacuuming now. Sounds like WW3.
Source please take note: In my New Earth there is only soft natural noise, telepathy, nice looking animals, friendly higher beings, blue skies and only to the point questions from others who respect and love eachother.
LikeLiked by 4 people
@777 Yes, I think we are all getting sick to the back teeth of this ‘realm’. It is getting harder and harder. It seems that the only choice is to be reclusive and not go out into the madness. I wonder what is the point of it all today..
I bite my lip when people speak about the news, the world and their obvious absolute belief in this ‘illusion’. If I say anything I will be seen as a loony! People have free will of course and the right to do what they want but it is so frustrating to sit by and watch, feeling helpless to do anything to change our situation because nobody wants to ‘wake up’. Usually try and be upbeat, let them all get on with it but am tired of it all today…Like you say CATS & Ms you can lead a horse to water, but you cannot make it drink…
I cannot think that anything is going to change unless we get outside help. if not:
‘Stop the world, I’m getting off…”
Love, Light ❤️
LikeLiked by 2 people
P.S I do apologise, I’m a real ‘grump’ today (PMT and just exhausted) will return when I have switched my light back on! ❤️
LikeLiked by 1 person
No worries Lily, you’ll still win the Ms. Congeniality award when all’s said and done. 🙂 Appreciation will lift you out of the funk — I’m feeling gratitude for the Stone Roses ~ thanks for posting! xo, Laura
LikeLiked by 3 people
@ark2arcturus thank you 🙏 I am grateful for your words, so much love ❤️❤️❤️
LikeLike
No need to apologize Lily, except for the Stone Roses, don’t like them. 😉
I was feeling the same way last night and this morning. Had an afternoon nap, just woke up and feeling completely different. And guess what: I sold my electrical guitar. Easiest sale ever, guy didn’t even want to test it, I’m sending it by mail tomorrow. He transferred the money this afternoon and it’s already on the account. Weird. Because it came from another country!
Little miracles! Ooh the incidents I’ve had selling stuff, not gonna tell but it’s a trilogy if I do write it. But hey, let’s focus on the miracle!
And remember Lily: we didn’t come here to fit in, we were never meant to, we’re here to change the Planet. Onwards, comrads! Onwards!
LikeLiked by 3 people
@777, wise words, thank you! Those dark moments can so quickly change, I need to remember that. It can be a lonely place to be but then you see just how enormously amazing our purpose is 🙏
Congrats for your guitar sale 🎸and apologies for stone roses 😉
Yep, onwards and upwards! Much love ❤️
LikeLiked by 1 person
Wow! TWBs are back (for many of us). They flew by low-and-slow last two nights in their distinctive diamond-shaped ship (looked at from top or bottom) about 100 feet off the deck over some of our respective houses. But they brought in reinforcements from somewhere, with a different look and different tactics. They aren’t exactly Tall White Bastards, anymore. Whereas before they’d appear in our dreams looking about 8-feet tall and rather bloated and thick and dead white and bald — like an ambulatory beluga whale, very easy to spot — now they’re REALLY tall (20 feet!) and have black hair and black eyes and long black fingernails… looking vaguely Goth-Polynesian… and of course they’re also actively attacking us, now… in a rather attractive 20-foot-tall homicidal tiki-giantess kinda way. They’ve also updated their wardrobes (?), wearing bright Hawaiian-style shifts, upgrading their look, apparently. They were chasing us and knocking over furniture and roaring, but we escaped in a rather unique way: if we held still, they couldn’t see us — even when they were looking right at us. We were vibrating too fast for them to see, even with their fancy instruments!
CATs need a vacation.
-CAT Eds.
LikeLiked by 7 people
They are so lame. They ALWAYS fly by on Tuesdays and Wednesdays, between 10 and 11:15 pm. Is this some kind of magic time? And what you left out: LOVE thoughts activate their shields! Very interesting.
At the behest of ~AM, I thought: “Love and healing light to you, brothers”… and their ship vanished. Five seconds later… they’re back. I did it again… and their ship vanished. Ha!
~M5
LikeLiked by 9 people
Yes, it’s the strategy I didn’t use last night with that ugly Gremlin. I still use attack mode, which is outdated both in ending it and from a higher perspective. Gonna work on that love thing. Thanks again.
LikeLiked by 1 person
I dreamed of flying gremlins and they said they ran into a big ghost in my bathroom and were scared of it. I told them just don’t come in here then lol.
LikeLiked by 2 people
I hope I never see them like that in broad daylight. It was terrifying.
-CAT3
LikeLiked by 2 people
Well, we WERE in their HQ! That’s why they were so big: home turf, where the bigger ones live. Funny how they’re purely matriarchal; the males won’t fight at all. Today’s feminists would love the TWBs… until they tried to kill them. That big one in the conference room knocking over all the furniture… hooboy, she was pissed. Dark flashing eyes. A babe, too. You’re beautiful when you’re angry!
~M6
LikeLiked by 3 people
If we hadn’t discovered that they couldn’t see us when we held still, we’d be goners. They were reeeeally motivated to get us last night, wow.
-CAT4
LikeLiked by 4 people
Blimey, you CATs had it rough last night, thank goodness you’re all okay! ❤️
LikeLiked by 6 people
And Ms too. Sounds terrifying! Do you think they were trying to use the equinox energy etc to attack? Phew! ❤️
LikeLiked by 2 people
We shall send blinding bright Lovelight to All. Peace.
LikeLiked by 3 people
I thought it was only me!
I noticed that dream infiltration started up again on the 19th – with a freaking vengeance! I had not had that happen for months. Of course I ALSO had surgery on the 19th, so I came home from the hospital in physical pain, holding ice packs to my side and unable to take care of myself, and then, at the same time, went through spiritual attacks that night and all nights since. Wtf.
It has not been fun, nor “pretty”. I am aware that the visuals and other crap were implanted, as that’s their MO…yet still to the mind they are so damned disturbing.
BUT –
During all of this I have seen the other side fighting back with some serious 🔥 firepower. It was truly humbling. I saw Brother J and others and the light they fight with, in a more literal way that I’ve ever experienced. Talk about magnificent, glorious, and invincible….I would not want to be on team dark for anything.
Anyway, thank you 🙏 🐈 cats, for that visual of a 20 foot tall Very Tan Tiki giantess…a grass skirt and hula dance immediately added theirselves to that visual in my mind, and I could not stop laughing! Xoxoxo ⚡️✨💜🌊
LikeLiked by 1 person
They stepped things up because we’re close to reaching some new level. We’re trying to quantify it at the time of this writing.
-CAT Eds.
LikeLiked by 3 people
Glad I’m not the only one fighting off bad guys! I thought maybe my protection wasn’t strong or efficient enough. I wake many times during the night and re-set my boundaries after these “attacks” or interactions. Thankfully it’s not every night😬
LikeLiked by 3 people
Yup. Us, too. One day… we’ll all sleep in. 😉
-CAT Eds.
LikeLiked by 3 people
Fortunately I have never had this.
Though I sometimes have a funny experience when i sometimes have a thought of a negative being showing up. I just think to the being “I see the food has arrived” (or something that would terrify anyone) and the feeling goes away as if utterly terrified.
I might have been their boss in a past life, lol.
LikeLiked by 1 person
I don’t have experience with any TWBs but have dealt with a variety of beings who don’t wish me well. Have experimented with various techniques usually while being attacked. I used to be attacked all the time for years, but not so much now. Last experience i posted here – that creepy ca$al woman at the train station with her bad mojo. Maybe I’m in retirement? Ha no chance.
Thanks Cats and M’s for your service and this blog. I don’t post much but check daily. Keeps me checked and in humour.
Are we there yet?
LikeLiked by 3 people
Did you remember to wear striped track suits?
Even Taller Black and White Bastards, ETBWB; I’m fine with just bastards.
~Sifoo
LikeLiked by 1 person
More than twice as tall as Kareem.
-CAT Eds.
LikeLiked by 1 person
Let’s hope that was their last resort attack. Stand invisible and know you are surrounded with unconditional love from Source and your Cat kin. Cay
LikeLiked by 5 people
I have been re-reading the comments, and it seems to me there is a lot of tension, hence misunderstanding abounds, too.
Everything is all right.
If people don’t listen/read/comprehend, it’s their choice.
Turn to source for divine love.
Who cares about the Schumann spikes? The device cannot measure the full potential of the Earth’s heartbeat, it hasn’t been designed to do so, it was designed in the old energy.
Love,
LikeLiked by 7 people
HI CATS! ARE YOU GETTING THIS DATA???
VERY #POWERFUL #INFLUX OF #ENERGY WILL STRIKE THE WEAK #MAGNETOSPHERE ON 22nd to 25th March 2019
**URGENT**
cropped-solar-energy-alert.png
VERY POWERFUL INFLUX OF ENERGY WILL STRIKE THE WEAK MAGNETOSPHERE ON 22nd to 25th March 2019. FURTHER EARTHQUAKES, VOLCANO ACTIVITY AND ADVERSE WEATHER WILL BE GREATLY INFLUENCED BY THE COSMIC RAYS STRIKING THE EARTH’S CORE
**BE ALERT**
AND THIS OF YESTERDAY MARCH 20TH:
#PROTON PARTICLES HAVE DRAMATICALLY INCREASED
**URGENT PROTON ALERT**
Proton Alert 20.03.19 11.13 hrs UTC
PROTON PARTICLES HAVE DRAMATICALLY INCREASED. FURTHER EARTHQUAKES, VOLCANO ACTIVITY & ADVERSE WEATHER PATTERNS WILL BE GREATLY INFLUENCED BY THE COSMIC RAYS STRIKING THE EARTH’S CORE
***BE ALERT***
BY THE WAY ARCHANGEL MICHAEL AFIRMS THE EVENT AS OF THE SHIFT TO NEW EARTH IS DURING THIS MONTH OF MARCH, DON’T DESPAIR AND GET READY FOR A LIFT OFF! AMEN! PATRICIA HELEN
LikeLiked by 7 people
Yeah, that’s those flares/CMEs. We never despair.
Mark our words: volcanoes and weird weather and earthquakes all occur *right before* The Event.
-CAT Eds.
LikeLiked by 6 people
One of the CATs wrote “SHARP LEFT” on our calendar… for today.
-CAT2
LikeLiked by 5 people
I think I got whiplash on that left turn. What a headache/neck tension/nausea laden afternoon. Better now, but not expecting much sleep tonight. As I was reclined this afternoon, I could feel my molecular structure start to vibrate faster than ever before. Lift off could be any time now. Love the fractal photo sent by Cheesy Kitten. Cay
LikeLiked by 2 people
I’ve been helping a friend at his business, and we were outside yesterday morning. There were many people around, and it was noisy. I started feeling woozy and had to sit down. As I sat, a golden moth flew in front of me and landed at my feet. I started slipping in and out – here and there (whatever that is). At one point when I slipped back here, I was looking across at several people and saw the whole scene spark/shift/jerk/whatever you might call it. Then I was slipping back and forth, and again I came back and saw the same thing again. The people did not seem to be aware, but I sure was. Then the moth flew up, fluttered around and flew away. I still felt a little woozy but was able to continue on with my day.
-CAT7
LikeLiked by 8 people
What time was that? Curious to know.
LikeLike
Around 10-11:00 am, US Central Standard Time.
-CAT7
LikeLike
Found some other people have seen rainbow circles too 🙂 https://in5d.com/incoming-plasma-waves/ though mine were just in my dreams.
LikeLiked by 5 people
Sorry to tell you, those rings around the sun are from humidity. They are very common here in the hot, humid summers. You can also see them in winter, if there’s enough water in the atmosphere.
LikeLike
@ Anonymous
2019-03-21 AT 10:17 PM
NO.
https://terrancognito.blogspot.com/2019/03/delegations-join-conversation-with-thor.html
LikeLike
Folks… it doesn’t matter what you see. That’s why it’s called, “perception.” When you see SOURCE let us know. 😉
-CAT Eds.
LikeLiked by 2 people
@anonymous, Nope. I am fully aware of humidity halos. This halo was clearly delineated almost as if it had a line outlining it. It lasted for about 5 minutes then was no longer visible.
LikeLiked by 2 people
I woke up at 5:57 am EDT this morning sweating, with my heart pounding out of my chest and a feeling of angst. I am unable to read the time(s) of the meters that you post but wonder if my episode corresponds to those fluctuations. I have been feeling nauseous with body aches in my back and neck all day. I had stayed up late last night reading the Q drops and seeing the pictures of the vile human trafficking associated with the Epstein island case. Surely that’s just a drop in the bucket of all that goes on world wide. It took me much clearing and meditation to fall asleep after that. Please Source! We need an end to the pain and suffering of Gaia’s populace! If nothing else, please save the children!
LikeLiked by 4 people
Visit with Lisa Friday morning. I’ll ask her about left turns among other things. I’ll report back.
LikeLiked by 2 people
Here we go; me thinks something big is incoming, ear ringing just got a new meaning. And my heart is doing back flips. The anxiety I was picking up earlier just switched into excitement, which only makes sense once there’s no turning back. Good thing I have plenty of coffee and newly baked chocolate chip buns, this is turning into an intense night.
~Sifoo
LikeLiked by 4 people
It’s a beautiful day here in Parmesan land. Skies as clear as they could possibly be, not a single trail or related weirdness sighted. Good vibes all around.
From what little I can sense (too much energy x_x), it seems Spirit is still preferring to move/advance the timeline by very small increments rather than initiating the huge SHIFT we were all anxious for. For what reason, your guess is as good as mine.
All is well. We’ll wait and see.
LikeLiked by 2 people
Out of curiosity, how much does a wedge of real parmesan cost there?
-CAT5
LikeLiked by 3 people
Right now, for the most typical Parmigiano, you’d spend around €13 to €14 for a 1-year-aged wedge. Of course, the more it ages, the more expensive it gets. I’ve seen some Stravecchio (3+ years!) wedges go for €19, even up to €20 for its more pricey variants.
The actual national price per kilogram is officially listed at €10,95 though.
Here, in its province of origin, Parmigiano Reggiano is treated as serious business. 😉
LikeLiked by 3 people
https://wakeup-world.com/2019/02/17/10-life-lessons-you-can-learn-from-your-cat/
10 Life lessons you learn from your cat :
1. Keep a curious spirit and approach uncertainty with a positive attitude.
2. Physical touch is natural, and vital for our wellbeing.
3. Get plenty of rest, and spend time soaking up the sun.
4. Show gratitude. All it takes is a purr, a squinty smile, or a dead mouse at your feet.
5. Stretch regularly. It’s good for body and soul.
6. Live in the moment. There is only now.
7. Play. Play. Play. Play. Play!
8. A happy life is a simple life. All we really need is love, a full belly, and a quiet place to rest.
9. Let the inner wisdom of instinct and intuition guide you. If it doesn’t feel good, walk away.
10. Be fearless. Live like you’re on your ninth life.
LikeLiked by 7 people
@ Bev 37. I read this too and loved it. Thank you for posting it here. I can’t figure out how to post anything other than my comments and was going to type it out. Cat’s/CATS can be very wise mentors.
LikeLiked by 1 person
Lisa said that the “left turn” signifies new life events in both the individual and the collective. Totally new and will be what the soul requires for growth. Stay tuned for this to become more readily apparent in April. The curtains have been closed for her these past 5 days due to the equinox energies. To be continued Sunday. Hopefully she’ll be able to see the results of my experiences the past few days. That’s all I know for now.
LikeLiked by 4 people
@oro
Thank you for your reply! Unfortunately, I’m more confused now than before, because my gut feeling with “The One” was never a good one and I was surprised, as I read the new “Guardian” messages, how well it fits my view on things. Now that wouldn’t be a big deal for me, but you wrote, that “…it’s quite the opposite of All we All know to be true”! That is quite a broad statement, but it doesn’t help much in terms of recognizing the deception, if there is one. It may not be the message that we want to hear, but that’s of course not what you are talking about, so I really wonder, what I’m missing here…
LikeLike
@ Mr K
thank you for your answer
not such a big deal
just my own perception
you are free to have yours
LikeLike