
Yeah. We know.
Put simply: We don’t believe anyone anymore.
Blossom’s latest about the monoliths… sorry, but those things are fake, it’s someone’s private joke. We don’t know who Blossom is talking to or what they’re talking about, but we don’t see what they’re seeing… and that makes us not want to listen to anything else from her. No offense. (We didn’t want to say anything, but CATs had stopped saying her mantra back in July because it felt like it was a tracking thing; now, we say, “Love and Light to all” at the end of the G+P+C process.)
While Laura Whitworth’s videos are still worthwhile, we don’t watch anything/anyone else, preferring to keep our own (limited) counsel. Note that we will not allow videos in the comments sections anymore, as that same dark faction that’s been active for so long is still down there and is trying to keep the dark alive through any means necessary, using some group (of 50) on the surface to broadcast… and it’s leaking into lots of unicorns. Watch that stuff if you want, it’s your choice, but not here. Meanwhile, the MSM chose today to crank up their “hope has arrived” crap about their slow-death shot. No, thanks.
Anyway, meterage. Meters either look either blank, or inexplicable… but, as you will see, the “KNOCK” is back:

KNOCK has so far mostly been detectable closer to Portal One inside the sun, thus:
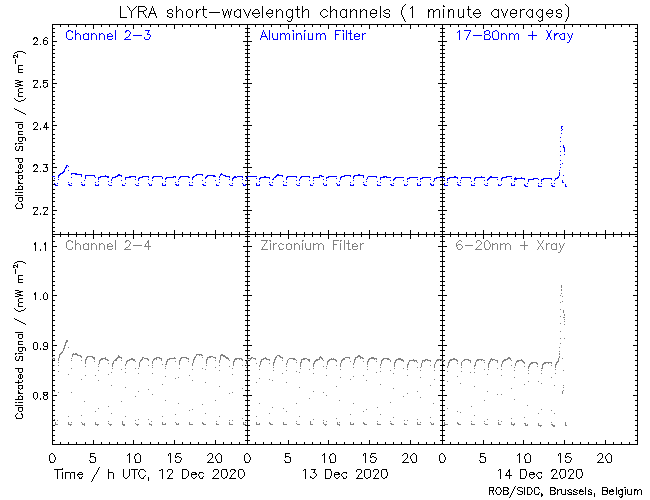
KNOCK has been in Italian meters for a while:



Whatever is coming is getting closer — closer than it’s ever been. The fact that we’re getting KNOCK in fairly UNsensitive meters is telling.
Anyway, yeah. We might be a little down this morning, given the state of things… everywhere… but in our (blah) eclipse/new moon meditation this morning… we all heard this theme (some had heard it a day or two before, but not mentioned it):
Considering the state of things, we’re going to hang our hats on that, at least till the solstice. YES, this is all Illusion, but we’re still sitting in the middle of a movie we’d rather avoid, thank you.
And ok, we also hear this sometimes, too:


UPDATE1
The KNOCK finally broke:

UPDATE2
Oh no…
…a gynormous SPACE SQUID has exited the sun and is heading to earth! It is coming to EAT all those who have been bad over the past year; the chomping sounds should be epic, but… it’s a messy eater so you might want to avert your eyes. And for SOURCE’S sake, DO NOT MAKE EYE CONTACT WITH THE SPACE SQUID. That’s what it wants you to do. Yes, we’re kidding. Like Justice, the SPACE SQUID has no sense of humor.



I hope that this the truth 🙂🙏✨
“Georgi Alexandrov Stankov, December 17, 2020
The global shift has commenced. The 21.12.2020 portal was fully opened yesterday evening. The ascension energies and vibrations are off the scale and very uplifting. The last two weeks of this year will be the most transforming in the history of humanity and this earth. Cancel all your plans and social activities, stay at home and meditate. There is nothing else you can do as everything is ready now for the shift.
The shift will be all-encompassing and will transform this reality radically. Most people will be in shock and panic. We will be called to explain what has happened – as ascended masters and as awakened informed individuals on the ground. There will be a lot of help from the higher realms.
That’s all for the time being…”
From here:
http://www.stankovuniversallaw.com/
LikeLiked by 5 people
The Shift commenced a while ago, where’s he been?
< CAT Eds.
LikeLiked by 8 people
Well, at 4:00am PST, I was bolt upright awake. The background energy which I always hear had changed once again. Mercy it was intenser! Har! Otherwise, same-o-same-o (tongue firmly in cheek)
LikeLiked by 7 people
Yup, we did that, too.
< CAT Eds.
LikeLiked by 7 people
Ha! J that was probably about the time I finally said “enough” – couldn’t sleep ’til about then and finally insisted my body get some zzzzs.
Kg
LikeLiked by 1 person
And another big GRB.
http://earthboppin.net/talkshop/space/messages/45201.html
LikeLiked by 6 people
~ CAT Eds. ~ Unusual readings on Cumiana European Lightning index , only 12! just now. It has been showing less and less activity over past several days. How does this relate to what is in progress energetically, if it does?
Kp levels are at Zero a lot lately too. I’m noticing continual heart/ body effects also for at least a week now. All part of the ongoing energy build?
Thank you.
Love, friend
LikeLiked by 6 people
Note the sun sprouting legs and trying to get away;-) The cat nail-filing is good, too. Thx for the reality; yr certainly right abt the chems… If I see another “great sunset/rise” posted as a pict, I’ll die.
LikeLiked by 4 people
Not Yet, We’re just getting to the Good part! Have a Most Joyous weekend. Peace.
LikeLiked by 1 person
Wow that was odd. I just wrote an incredibly long comment but after I clicked submit my comment didn’t appear. Grrrr… well I’m not writing all that over again. Anyways, just wanted to say great blog!
LikeLike